HYDRODYNAMIQUE NAVALE

HYDRODYNAMIQUE NAVALE

L’hydrodynamique navale, qui traite des rapports du navire avec l’eau qui l’entoure, constitue sans nul doute l’une des disciplines fondamentales que doit maîtriser l’architecte naval au moment d’élaborer un nouveau projet. Ces rapports conditionnent en effet très directement non seulement les formes et les dimensions principales de la carène, mais aussi la puissance de l’appareil propulsif, celle de l’appareil à gouverner, l’échantillonnage de la charpente... Les enseignements de l’hydrodynamique navale sont également utiles au marin qui doit pouvoir diriger son bâtiment quels que soient l’état de la mer et les obstacles à éviter.

Si ses origines sont donc aussi anciennes que les navires eux-mêmes, l’hydrodynamique navale ne s’est toutefois établie comme science qu’à partir du XVIII^e siècle. Elle eut alors la bonne fortune d’intéresser des savants aussi prestigieux qu’Euler, Bernoulli, Bouguer, d’Alembert ou Condorcet. Entre autres problèmes, ils se posèrent évidemment celui de la résistance à l’avancement des vaisseaux, non pas tant d’ailleurs pour prévoir les performances d’un navire en construction, que pour trouver une carène de navire de moindre résistance qui, selon les idées émises par Newton dans ses Principes , devait nécessairement être de formes géométriques simples. Les connaissances sur les causes de la résistance faisant alors à peu près complètement défaut, on entreprit des études expérimentales en remorquant, sur des bassins existants, des modèles réduits très schématiques. Les travaux les plus intéressants furent exécutés en Angleterre par Fortney et Beaufoy, en Suède par Chapman, qui fut un éminent architecte naval, et surtout en France. D’Alembert, Condorcet et l’abbé Bossut notamment exécutèrent en 1775, à la demande de Turgot, des essais tendant à évaluer l’augmentation de la résistance lors du passage d’un bateau en canal (cf. gravure). Quant à Romme, il fut l’un des rares à exécuter des essais sur une maquette conforme à un vaisseau réel, l’Illustre (Rochefort, 1785).

Quelques-uns, Euler entre autres, pressentaient déjà le rôle que pourraient jouer ces essais à échelle réduite pour le dessin des navires; cependant, il fallut encore attendre un siècle pour que, les lois de similitude étant maîtrisées, la technique des modèles entrât dans les applications pratiques. Le Français Ferdinand Reech, qui se consacra entièrement à l’enseignement de l’architecture navale, énonça dès 1832 que «les résistances de corps flottants de formes semblables ne peuvent être proportionnelles aux surfaces et aux carrés des vitesses qu’autant que les carrés des vitesses sont proportionnels aux dimensions linéaires». L’Anglais William Froude compléta cette proposition en distinguant les différentes causes de la résistance, et il réalisa la première expérience convaincante: la résistance à la marche du Greyhound , mesurée au cours d’un remorquage à la mer (1873), fut en effet trouvée supérieure de 10 p. 100 seulement aux prévisions faites à partir des essais sur modèle qu’il avait effectués dans le bassin, construit tout spécialement pour lui par l’amirauté britannique, à Torquay. La méthode des modèles était née. Cette méthode expérimentale d’approche de l’hydrodynamique navale se révéla vite très puissante. L’exemple de l’Angleterre fut peu à peu suivi par toutes les nations maritimes, la France se dotant pour sa part, sous l’impulsion d’Émile Bertin, d’un bassin d’essais de carènes en 1906.

Ces bassins furent d’abord tous du type canal, c’est-à-dire suffisamment allongés (plusieurs centaines de mètres dans la pratique) pour permettre de mesurer sur une assez grande longueur la résistance, puis les performances propulsives et le comportement sur houle de l’avant ou de l’arrière. Des installations spécialisées naquirent ensuite: tunnels dépressurisés à circulation d’eau pour l’étude de la cavitation (le premier fut construit par Parsons en Angleterre au début de ce siècle); cuves spécialisées pour l’étude du navire sur une mer venant d’une direction quelconque, régulière puis irrégulière; bassins spéciaux pour l’étude de la manœuvrabilité...

Au total, il n’est guère de phénomène relevant de l’hydrodynamique navale qui ne puisse faire aujourd’hui l’objet d’une approche sur modèle réduit.

Si le développement de l’hydrodynamique navale repose donc très largement sur l’expérience, il s’appuie aussi, et de plus en plus, sur la théorie. En particulier, la formation des vagues de surface par le navire, problème spécifique de l’hydrodynamique navale, a suscité depuis l’origine, et suscite encore aujourd’hui, l’intérêt le plus marqué de la part des meilleurs spécialistes. Les travaux sur le sujet ont d’ailleurs conduit à la mise au point de méthodes tout à fait originales.

Les intersections avec d’autres disciplines sont grandes pour certains problèmes: c’est ainsi que les méthodes de calcul des hélices marines, et des surfaces portantes en général, ont largement profité de l’effort important réalisé en aérodynamique.

Dans tous les cas, la théorie progresse au même rythme que les moyens de calcul, c’est-à-dire exponentiellement, et l’on peut optimiser les projets avec une bonne approximation, l’expérimentation sur modèle continuant à jouer un rôle important dans la vérification des lois élémentaires et la prévision des performances globales du navire. Quant aux essais à la mer, ils restent certainement l’arbitre ultime auquel s’en remettent traditionnellement constructeur et armateur du navire.

1. Résistance à la marche et dessin des formes de la carène

Si l’étude de la résistance à la marche – c’est-à-dire l’étude des forces qui s’opposent au mouvement d’avance du navire – a constitué pratiquement pendant de nombreuses années l’unique chapitre de l’hydrodynamique navale, elle demeure encore aujourd’hui fondamentale car elle conditionne très largement le choix des formes de la carène.

Les composantes de la résistance; la «méthode des modèles»

Mis à part la traînée des superstructures, relativement faible (2 à 3 p. 100 du total) et d’ailleurs facile à calculer compte tenu du fait qu’il s’agit de corps à arêtes vives, ces forces ont essentiellement deux causes: la présence d’une surface libre d’une part, la viscosité de l’eau d’autre part. Avec une bonne approximation on peut admettre – hypothèse de Froude – que ces deux causes sont indépendantes.

La «résistance de vagues» R^w est sous la dépendance du nombre de Reech-Froude face=F9796 F = V / 連g L (avec g l’accélération de la pesanteur, L la longueur du navire, V la vitesse), ce qui signifie que, à face=F9796 donné, le coefficient de résistance de vagues R^w / (avec le déplacement du navire) ou C^w = R^w /(1/2) 福SV ² (avec 福 la masse volumique de l’eau, S une surface de référence appelée surface mouillée de la carène) est le même pour deux carènes semblables.

La «résistance visqueuse» R^v dépend de son côté du nombre de Reynolds face=F9796 R = V L/ 益 ( 益 est la viscosité cinématique de l’eau égale à 1,1 . 10^-6 m²/s) et de la rugosité relative de la carène qu’on caractérise par un rapport k /L, où k est le diamètre des grains de sable qui, collés sur la carène, produiraient le même effet que la rugosité réelle.

Au total, le coefficient de résistance hydrodynamique est de la forme:

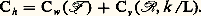Pour prévoir la résistance hydrodynamique d’un navire, on procède en général à des essais sur modèle réduit. Il faut en principe réaliser à cet effet l’égalité, pour le modèle (m ) et pour le navire (s ), des paramètres sans dimension face=F9796 , face=F9796 R et k /L; mais on s’aperçoit immédiatement que les trois conditions correspondantes sont impossibles à réaliser simultanément, à moins évidemment de travailler à l’échelle 1!

Pour passer outre à cette impossibilité théorique, on a recours à un artifice dû à Froude: on se place en similitude de Reech-Froude (face=F9796 F^{m =} face=F9796 F^s , d’où C^wm = C^ws ) et l’on fait une correction pour tenir compte de la non-égalité des nombres de Reynolds du modèle et du réel. On a alors C^hs = C^hm 漣 (C^vm 漣 C^vs ). La «correction de frottement» qui permet de passer de C^hm à C^hs est négative compte tenu que face=F9796 R^m 麗 face=F9796 R^s ; elle est, en valeur absolue, comprise entre 0,15 et 0,25 C^vm .

Ordre de grandeur de la résistance à la marche

La figure 1 fournit, pour les navires classiques de surface, l’ordre de grandeur de leur résistance hydrodynamique «spécifique» R^h / et la part prise par la résistance de vagues dans cette résistance hydrodynamique, en fonction du nombre de Reech-Froude face=F9796 d’utilisation. On notera l’influence considérable de face=F9796 sur la résistance: R^h / est par exemple cent fois plus grand en moyenne pour une vedette que pour un pétrolier.

La résistance des sous-marins en surface est, à face=F9796 donné, sensiblement plus grande que celle qui est indiquée par la figure 1. Cela tient à ce que les sous-marins modernes, avant tout dessinés pour la navigation en plongée, sont de médiocres navires de surface.

La résistance des navires rapides non classiques, hydroptères ou aéroglisseurs marins, est difficile à analyser dans les mêmes termes.

Résistance visqueuse. Importance de l’état de surface de la carène

Comme on l’a vu plus haut, la connaissance de la résistance visqueuse est nécessaire pour pouvoir appliquer la méthode des modèles mais, malgré les progrès réalisés dans le calcul des couches limites tridimensionnelles, il n’est pas encore possible d’effectuer un véritable calcul complet de l’écoulement autour d’une carène de forme quelconque; on a donc recours ici encore à des approximations, d’autant plus justifiées d’ailleurs que le coefficient C^v de résistance visqueuse n’intervient en fait que par la différence des valeurs qu’il prend pour le navire et pour le modèle.

Pratiquement, la résistance visqueuse de la carène est celle d’une plaque plane rugueuse qui aurait même longueur et même surface mouillée, multipliée par un coefficient de forme compris entre 1,05 (navires très rapides) et 1,25 (gros pétroliers par exemple).

L’analyse de la résistance visqueuse met en évidence l’influence sensible de la rugosité de la coque, qui dépend elle-même essentiellement de la peinture utilisée et du soin avec lequel elle a été appliquée. La rugosité k d’un navire neuf pouvant varier en gros de 0,1 à 0,3 mm, on peut constater des différences de résistance totale considérables pour des navires réputés identiques, à leur état de surface près; des différences de 20 p. 100 au moins ne sont pas exceptionnelles dans le cas de navires gros et lents, pétroliers par exemple.

De même, l’accroissement de la rugosité de la coque au cours de la vie du navire explique la nécessité de procéder à un «carénage» – c’est-à-dire de la nettoyer et de la repeindre – à intervalles réguliers (tous les ans ou tous les deux ans) de manière à lui redonner son niveau initial de performances.

Tout ce qui vient d’être dit jusqu’ici suppose implicitement que la carène est suffisamment bien profilée pour qu’il ne se produise pas de décollement dans l’écoulement. S’il n’en est pas ainsi (navires aux formes arrière pleines), la résistance visqueuse est majorée d’une «résistance de remous» difficile à calculer. Des remous peuvent aussi être provoqués par les appendices de coque du navire: pour un navire moderne, la résistance des appendices peut représenter jusqu’à 15 ou 20 p. 100 de la résistance de la carène nue, et même jusqu’à 100 p. 100 pour un sous-marin en plongée périscopique.

Résistance de vagues

Un navire qui se déplace à la surface de l’eau engendre un champ de vagues dont les caractéristiques essentielles, quand le mouvement est permanent, sont les suivantes (cf. photos):

– le champ de vagues est fixe par rapport au navire;

– il n’intéresse qu’une partie de la surface libre, au voisinage du navire et sur son arrière; à quelque distance sur l’arrière du navire les vagues sont contenues dans un angle de demi-ouverture de 20⁰ environ si la profondeur d’eau est grande;

– dans cette zone, on peut assez aisément distinguer deux systèmes de vagues, des «vagues transversales» et des «vagues divergentes», qui viennent se confondre sur les bords du champ;

– dans le cas d’une carène comportant une partie cylindrique développée (pétrolier par exemple), le champ de vagues apparaît comme la superposition de deux champs élémentaires issus, le premier de l’avant du navire, le second de l’arrière.

L’existence d’une résistance de vagues R^w , même pour un navire en mouvement uniforme dans un fluide parfait, et ses caractéristiques essentielles découlent de l’existence et des caractéristiques du champ de vagues.

En fonction du nombre de Reech-Froude face=F9796 , le coefficient de résistance de vagues C^w présente des oscillations (fig. 2) qui sont dues à l’interférence entre vagues de l’avant et vagues de l’arrière. Quand les vagues transversales de ces deux systèmes sont en phase, elles ont tendance à se renforcer: l’énergie totale du champ de vagues, donc le coefficient de résistance C^w , passent par un maximum; c’est l’inverse qui se produit quand les vagues transversales sont en opposition de phase. Les valeurs de face=F9796 favorables et défavorables dépendent essentiellement de la répartition longitudinale des volumes, c’est-à-dire du rapport du volume de la carène au volume du cylindre longitudinal circonscrit.

La théorie confirme qualitativement les résultats fournis par l’expérience mais, malgré des progrès indéniables depuis Michell (1898) et l’emploi de calculateurs de plus en plus puissants, il est encore impossible de calculer la résistance de vagues d’un navire de formes courantes avec une précision telle que l’on puisse se passer d’essais de modèles.

La méthode de base la plus couramment utilisée pour calculer R^w est la méthode de Havelock (1932) qui consiste à remplacer la carène par des singularités mathématiques du type sources (ou doublets) distribuées sur sa surface. On prolonge mathématiquement l’écoulement au-dessus de la surface libre en remplaçant celle-ci par des sources images de manière à satisfaire aux conditions aux limites; on montre que cette assimilation carène-sources est non seulement valable du point de vue cinématique (le champ de vagues calculé loin sur l’arrière de la carène est très semblable au champ de vagues mesuré) mais également du point de vue dynamique, les forces de pression sur la carène étant ici remplacées par les forces qui s’exercent fictivement sur les sources qui constituent la carène proprement dite.

Formes de carène

L’expérience aussi bien que la théorie montrent l’importance fondamentale du nombre de Reech-Froude pour le tracé des formes de carène. En gros, on peut distinguer trois types de navires selon leur degré de vitesse:

– Si face=F9796 est petit (cas des pétroliers, des minéraliers, des cargos lents), les interactions entre vagues de l’avant et de l’arrière sont faibles, et l’on peut adopter des formes conduisant à un coût de construction faible, c’est-à-dire des formes pleines comportant une partie cylindrique d’autant plus développée que face=F9796 est petit. La partie avant doit toutefois être suffisamment longue pour ne pas créer une vague d’étrave trop prononcée; l’adjonction d’un gros «bulbe», c’est-à-dire d’un renflement sous la flottaison, est également utile de ce point de vue. La partie arrière doit de son côté être suffisamment développée pour qu’il ne se produise pas de remous tourbillonnaires trop importants.

– Les navires qui naviguent au-delà du dernier «creux» de résistance (porte-avions, croiseurs, avisos, vedettes) sont encore relativement faciles à dessiner; plus face=F9796 est grand, plus les formes se tendent et, pour les navires naviguant au voisinage de la dernière bosse (face=F9796 F 力 0,5), le plus important est de réduire au minimum la surface du maître-couple.

– Les navires (cargos rapides, porte-conteneurs, paquebots) qui naviguent entre l’avant-dernière bosse et le dernier creux (face=F9796 F 力 0,3-0,35) sont en revanche difficiles à dessiner en raison des interférences entre vagues de l’avant et de l’arrière; leurs formes, nécessairement galbées, sont généralement améliorées par l’adjonction à l’avant d’un bulbe, qui a pour effet de créer un système de vagues propre s’opposant au système de vagues de l’avant. On a même pu montrer théoriquement, et vérifier expérimentalement, que l’adjonction d’un deuxième bulbe à l’arrière – solution toutefois irréaliste – permettrait de réduire pratiquement à zéro la résistance de vagues d’un navire pour une valeur donnée de face=F9796 .

2. Propulsion

Définition et principe de fonctionnement de l’hélice propulsive

L’hélice, qui fit son apparition sur les navires au milieu du XIX^e siècle, constitue le moyen de propulsion le plus couramment utilisé.

Une hélice est essentiellement constituée par un certain nombre de pales (entre trois et six pour les navires classiques) qui ont en gros la forme d’ailes portantes hélicoïdales (pas géométrique H), et qui sont montées sur un moyeu généralement cylindrique. Les pales sont en général fixes par rapport au moyeu mais certaines hélices, qui doivent travailler dans des conditions de charge très variables (chalutiers, dragueurs par exemple), ont des pales orientables autour d’un axe normal au moyeu.

Quand l’hélice a une vitesse d’avance V ⁰ parallèle à son axe et une vitesse de rotation 諸 = 2 神 n (n étant le nombre de tours par unité de temps), ses sections cylindriques se comportent comme des profils d’ailes portantes; il en résulte un effort hydrodynamique qui se réduit au total à une poussée T parallèle à l’axe et à un couple Q autour de cet axe, soit un coefficient de poussée K^T = T/ 福n ²D⁴ (D est le diamètre), un coefficient de couple K^Q = Q/ 福n D⁵ et un rendement 兀 = V ⁰T/2 神n Q. K^T, K^Q et 兀 sont essentiellement fonction du «degré de progression» J⁰ = V ⁰/n D (fig. 3), mais dépendent en revanche relativement peu de la viscosité de l’écoulement.

Les courbes caractéristiques de fonctionnement de l’hélice dépendent fortement du pas géométrique réduit H/D: l’augmentation de H/D décale vers la droite les courbes (J⁰; K^T) et (J⁰; K^Q); la valeur de J⁰ pour laquelle K^T = 0 est très voisine de H/D, d’où son nom de «pas effectif». L’augmentation de H/D entraîne également un accroissement du rendement maximal de l’hélice.

Pour étudier théoriquement le fonctionnement de l’hélice, comme d’ailleurs celui des surfaces portantes en général, on remplace celle-ci par une distribution de tourbillons (ou une distribution mixte de tourbillons et de sources, les sources étant destinées à représenter l’effet d’épaisseur des pales); quand l’envergure relative des pales est petite, les tourbillons qui constituent l’hélice, encore appelés tourbillons «liés», se réduisent à une simple ligne tourbillonnaire; le modèle théorique est alors analogue au modèle de Prandtl pour les ailes portantes de grande envergure. La circulation autour des sections cylindriques de chaque pale étant variable avec leur distance r à l’axe, il s’échappe nécessairement du bord de fuite de chaque pale une nappe de tourbillons, appelés tourbillons «libres», qui, dans le modèle le plus simple, est un hélicoïde droit de pas V /n .

Le calcul de la circulation puis celui des efforts hydrodynamiques sont effectués en fluide parfait. L’effet de la viscosité, qui est essentiellement pour chaque élément de pale une force de traînée, est évalué séparément; il se traduit au total par une diminution de la poussée et une augmentation du couple, donc une diminution du rendement.

La théorie de l’hélice, même si elle procède par approximations successives en partant d’hypothèses simples, conduit à des résultats qui sont très proches de l’expérience.

Interactions hélice-carène

À cause de la présence de la carène, l’hélice ne travaille jamais dans un champ de vitesse relative uniforme: il existe un certain «sillage». Par exemple, la vitesse d’arrivée d’eau dans l’hélice peut être réduite à 20 p. 100 seulement de la vitesse de route V , si l’on se place dans le plan longitudinal juste sur l’arrière de l’étambot d’un gros navire à ligne d’arbres unique (le coefficient de sillage local, différence relative entre V et la vitesse locale, est alors de 0,8).

Les courbes caractéristiques de fonctionnement de l’hélice derrière la carène (J; K^T), (J; K^Q), avec J = V /n D, se déduisent des courbes de fonctionnement de l’hélice isolée par une affinité telle que J⁰ = J (1 漣 w ) . w , sillage effectif de la carène, est en quelque sorte la moyenne, effectuée par l’hélice, du sillage local sur tout son disque. w varie de zéro pour les vedettes rapides à deux lignes d’arbres à 0,4 pour les gros pétroliers à une ligne d’arbres.

De même qu’il existe une action de la carène sur l’hélice, il existe réciproquement une action de l’hélice sur la carène qui est une force de succion S (l’hélice aspire l’eau devant elle). La poussée effective T^e de l’hélice n’est pas alors égale à T, mais à T^e = T 漣 S = T (1 漣 t ), où t représente le coefficient de succion, qui varie de 0,05 pour les vedettes rapides à 0,3 pour les gros pétroliers à une ligne d’arbres.

On obtient le point de fonctionnement en autopropulsion en écrivant que la poussée effective T^e de l’hélice est égale à la résistance à la marche R.

Le «rendement propulsif global» 兀^g est défini comme le rapport P^r /P entre la puissance P^{r =} V R nécessaire pour remorquer la carène à la vitesse V et la puissance P = 2 神n Q appliquée effectivement sur l’axe de l’hélice. 兀^g peut être mis sous la forme 兀^g = 兀⁰ 兀^I, où 兀⁰ est le rendement propre de l’hélice isolée et 兀^I un rendement d’interaction fonction du sillage et de la succion. 兀^I varie de 0,9 pour les vedettes rapides à 1,4 pour les gros pétroliers à une ligne d’arbres. 兀^g dépend évidemment du rendement propre de l’hélice en place; il reste en gros compris entre 0,6 et 0,75.

Risques de cavitation

Quand, au sein d’un liquide, la pression descend au-dessous d’une certaine valeur qui, en première approximation suffisante pour les applications pratiques, est égale à la tension de vapeur e , le liquide se vaporise. La cavité ainsi produite grossit très rapidement en prenant des formes variables selon les conditions locales de l’écoulement; quand cette cavité, ou une partie de cette cavité, est entraînée par le courant dans une zone où la pression est plus grande, elle se résorbe brutalement – d’où le nom de collapsus donné à ce phénomène – provoquant un bruit intense et, le cas échéant, une érosion des corps solides qui se trouvent placés dans la zone de collapsus. C’est dire que, indépendamment même de la chute des performances qu’elle peut entraîner, la cavitation est, sauf exception, un phénomène nuisible qu’on cherche à éviter dans toute la mesure du possible.

En écrivant que la cavitation se produit pour p = e , on fait apparaître un paramètre sans dimensions nouveau 靖 = (p ⁰ 漣 e )/(1/2) 福V ² où p ⁰ est la pression statique. Comme la vitesse du modèle V ^m est généralement inférieure à la vitesse V ^s du réel, la réalisation de la condition 靖^m = 靖^s entraîne p ^0m 麗 p ^0s , c’est-à-dire que les essais de cavitation nécessitent d’opérer dans des installations placées sous vide.

Sur un navire on peut rencontrer de la cavitation en de nombreux endroits: sur l’étrave, sur les prises ou sorties d’eau, sur le gouvernail, sur les quilles de roulis ou sur les ailerons stabilisateurs et sur les chaises supports d’arbres, mais c’est surtout la cavitation de l’hélice qui conduit en général aux ennuis les plus sérieux.

La possibilité pour une hélice de caviter se comprend aisément si l’on se souvient que son rôle est de fournir une certaine poussée par différence de pression entre sa face arrière, ou «face», mise en surpression et sa face avant, ou «dos», mise en dépression. Pour une hélice bien dessinée et travaillant à son point de fonctionnement nominal dans un milieu indéfini, la cavitation qu’on peut normalement rencontrer est une cavitation par bulles isolées ou par nuage sur le milieu du dos (fig. 4). Si le degré de progression est inférieur à J⁰ nominal, une cavitation par lame sur le bord d’entrée côté dos (prolongée le plus souvent par un tourbillon d’extrémité) peut se produire prématurément; un tourbillon d’ogive apparaît également. Pour J⁰ 礪 J⁰ nominal, c’est au contraire une cavitation par lame sur le bord d’entrée côté face qui est à redouter. On peut diminuer le risque de cavitation en augmentant la surface de l’hélice mais c’est naturellement au prix d’une perte de rendement.

Les choses se compliquent quand l’hélice travaille derrière une carène. À cause des variations d’incidence, les figures de cavitation sur une pale donnée se modifient au cours de sa rotation. Au total, les risques sont augmentés.

Comme toute cavitation, la cavitation de l’hélice est génératrice de bruits et d’érosions. Les premiers sont particulièrement dangereux dans le cas des bâtiments de guerre dont la discrétion acoustique est actuellement l’une des qualités maîtresses; quant aux érosions, elles affectent toutes les hélices mais, il faut le noter, il s’agit d’un effet cumulatif qui n’est réellement gênant que si l’hélice travaille en permanence en régime de cavitation (fig. 5). Quand la cavitation est développée il se produit également une chute des caractéristiques mécaniques, poussée, couple et rendement, due au fait que la pression sur le dos ne peut descendre au-dessous de e ; cette chute des performances s’accompagne d’une augmentation du nombre de tours qui peut être gênante pour le moteur.

Il arrive un moment où, la vitesse augmentant, on ne peut plus éviter la cavitation; il est alors préférable d’en prendre son parti en essayant de limiter au minimum ses inconvénients. C’est ce qu’on cherche à faire avec les hélices «supercavitantes» qui ont un bord d’attaque aigu de manière à déclencher une cavitation qui recouvre le dos et se prolonge même en arrière de la pale. Les hélices supercavitantes ne suppriment pas les bruits mais elles évitent les érosions (puisqu’il n’y a pas de collapsus sur les pales); de plus, elles ont des performances meilleures que les hélices normales en régime de cavitation. Sur certaines hélices de ce type, on souffle de l’air sur le dos pour maintenir le régime de fonctionnement avec cavité même à faible vitesse; ces hélices «ventilées» ont l’avantage d’être moins bruyantes, l’air contenu dans la cavité se comportant comme un matelas qui atténue les collapsus.

Risques de vibrations

Le fonctionnement de l’hélice peut être à l’origine de vibrations de la coque selon deux mécanismes distincts, qui sont soit des vibrations par fluctuations de pression sur la coque (ou sur le gouvernail), soit des vibrations transmises par la ligne d’arbres.

D’une part, le passage des pales de l’hélice à proximité de la coque engendre sur celle-ci une dépression à la fréquence n Z (n est le nombre de tours, Z le nombre de pales) qui peut provoquer directement une vibration de la structure du navire. D’autre part, à cause des variations du sillage sur l’arrière de la carène, l’hélice est soumise à des efforts fluctuants (six composantes) qui se transmettent à la ligne d’arbres puis, par son intermédiaire, à la coque.

Les risques de vibration peuvent être très gênants pour les gros navires de charge à une seule ligne d’arbres. Pour les éviter, plusieurs mesures peuvent être prises. L’augmentation du nombre de pales de l’hélice et le déversement de celles-ci vers l’arrière constituent le seul remède généralement possible pour un navire en service. Au stade du projet, on doit de plus respecter des jeux suffisants, d’une part, entre l’hélice et le gouvernail, d’autre part, entre l’hélice et la coque et atténuer le plus possible les irrégularités de sillage par un dessin judicieux des formes arrière.

3. Tenue à la mer

Le comportement du navire sur mer agitée met en jeu un ensemble complexe de phénomènes de natures diverses: mouvements de plate-forme, embarquements d’eau, contraintes dans la charpente, résistance à la marche et performances propulsives. La mer réelle étant elle-même un phénomène aléatoire complexe, la tenue à la mer ne peut guère être traitée dans sa globalité. En s’appuyant sur le fait que les six équations du mouvement forment en première approximation deux sous-systèmes indépendants, on se contente en général de traiter du comportement du navire sur mer de travers d’une part, sur mer de l’avant ou de l’arrière d’autre part, en commençant d’ailleurs par admettre, pour simplifier, que cette mer se réduit à une houle régulière, ce qui n’est certainement vrai que dans des circonstances exceptionnelles.

Comportement du navire sur houle régulière de travers. Roulis

Le mouvement le plus important est celui de roulis, oscillation autour d’un axe longitudinal. Son équation, qui peut être en première approximation découplée des équations relatives à l’embardée et au lacet, traduit l’équilibre, autour de l’axe longitudinal Gx du navire, des efforts divers suivants: efforts de pesanteur (poids, poussée d’Archimède), efforts d’inertie, efforts hydrodynamiques décomposés eux-mêmes en efforts dus au mouvement du navire en eau calme d’une part, efforts exercés par la houle sur le navire animé de sa seule vitesse d’avance moyenne V .

L’équation du roulis se présente comme une équation différentielle du second ordre non linéaire. En fonction de la période de la houle, le rapport d’amplification 﨏⁰/ 﨑⁰ (avec 﨏⁰ l’amplitude du roulis et 﨑⁰ la pente maximale de la houle) présente un maximum aigu pour T voisin de la période propre T size=1^﨏 du roulis en eau calme: le roulis est essentiellement un phénomène de résonance. Pour une période de houle T grande, c’est-à-dire pour une longueur d’onde 炙 grande, le navire suit la houle: 﨏⁰/ 﨑⁰ tend vers 1 (fig. 6).

Les paramètres qui ont le plus d’influence sur le roulis sont:

– la stabilité statique du navire; plus elle est grande, plus 﨏⁰ est grand;

– la vitesse de route V du navire; quand V augmente, l’amortissement augmente, donc 﨏⁰ diminue.

Comme il s’agit d’un mouvement peu amorti qui met en jeu des efforts hydrodynamiques modérés, il est possible de réduire le roulis, soit en jouant sur l’amortissement visqueux (c’est le rôle des quilles de roulis qui fonctionnent en toute circonstance), soit en créant un effort antagoniste de l’effort dû à la houle. Ces stabilisateurs de roulis sont essentiellement de deux types:

– des ailerons mobiles placés de chaque bord et dont l’orientation est asservie au mouvement du navire; ils permettent de réduire le roulis à presque rien si la vitesse du navire est élevée, mais ils ne sont guère efficaces à petite vitesse puisque leur portance est proportionnelle à V ²;

– des citernes dont le rôle est de faire passer de l’eau d’un bord sur l’autre du navire avec un déphasage tel que le moment supplémentaire ainsi créé soit égal et opposé au couple perturbateur de la houle; ces citernes, généralement passives, ont l’avantage de fonctionner aussi bien à l’arrêt qu’en marche mais ont l’inconvénient d’augmenter le déplacement, et surtout d’exiger, pour être efficaces, une perte de stabilité statique.

Comportement du navire sur houle régulière de l’avant ou de l’arrière. Tangage

Sur mer de l’avant ou de l’arrière, la question du mouvement ne se présente pas tout à fait de la même façon que dans le cas précédent même si, au départ, les équations traduisent le même équilibre général entre efforts de pesanteur, efforts d’inertie et efforts hydrodynamiques. Les différences essentielles sont les suivantes:

– il existe un fort couplage entre le mouvement vertical du centre de gravité (pilonnement 﨣) et le mouvement autour de l’axe transversal passant par G (tangage );

– 﨣 et restant modérés, les équations du mouvement sont toujours linéaires;

– les termes d’amortissement sont grands; ils ne sont d’ailleurs pas de type visqueux mais tiennent à ce que les mouvements du navire en eau calme engendrent une houle complexe dont l’énergie est rayonnée à l’infini;

– le rapport 炙/L de la longueur d’onde de la houle à la longueur du navire n’étant pas obligatoirement grand, l’excitation de 1a houle ne varie pas de façon monotone; pratiquement nulle pour 炙/L 麗 0,6, cette excitation passe par un maximum pour 炙/L légèrement supérieur à 1 (fig. 6).

Au total, l’amplitude des mouvements ( 﨣⁰/(h /2), h étant le creux de la houle; ⁰/ 﨑⁰, 﨑⁰ étant sa pente maximale) peut être maximale dans les deux cas suivants. D’abord, dans le cas où la période de rencontre T^e de la houle (différente de T à cause de la vitesse d’avance du navire) est voisine de la période propre du pilonnement T size=1^﨣 ou de celle de tangage T size=1^﨏; il y a alors résonance, mais cette résonance est très atténuée. Ensuite, dans le cas où l’excitation de la houle passe par un maximum; ce phénomène est prépondérant.

Mer de l’avant, les deux phénomènes ont tendance à se renforcer, d’où des mouvements importants pour 炙/L compris entre 1 et 1,5, mouvements qu’il n’est d’ailleurs guère envisageable de réduire artificiellement compte tenu des forces en jeu; mer de l’arrière au contraire, la plage de résonance correspond à des valeurs de 炙/L petites pour lesquelles l’excitation est très faible, d’où des mouvements très modérés au total.

Mer de l’avant, cette plage de 炙/L critique pour les mouvements est aussi une plage critique pour d’autres phénomènes qui sont bien souvent aussi gênants: embarquement d’eau et mouille de l’avant, accroissement des efforts d’ensemble subis par la charpente du navire, slamming (c’est-à-dire mise en vibration de la coque due à une retombée brutale de l’avant dans la lame [cf. photo]), perte de vitesse due à une augmentation de la résistance à la marche et à une dégradation des performances propulsives. Certains de ces phénomènes ne dépendent, comme les mouvements, que des dimensions générales du navire; d’autres au contraire (mouille, slamming notamment) dépendent très largement des formes locales de la partie avant (des formes trop plates sont par exemple à éviter quand le slamming est à craindre).

Mer de l’arrière, on doit signaler la possibilité de mouvements d’embardée et de lacet dus à une instabilité de la tenue de route quand la célérité de la houle est un peu supérieure à V et que 炙/L 礪 1, ainsi que la possibilité de roulis très importants dus à un couplage non linéaire entre roulis et pilonnement ou entre roulis et tangage.

Comportement du navire sur mer réelle. Navigation météorologique

L’aspect chaotique de la mer réelle conduit à une approche probabiliste du problème. Compte tenu de la façon même dont elle se forme, cette mer peut être considérée comme la superposition d’une infinité de houles élémentaires d’amplitudes infiniment petites, de toutes longueurs d’onde et de toutes directions, la phase de chacune de ces houles élémentaires étant aléatoire et distribuée de façon équiprobable sur tout l’intervalle [0; 2 神].

Globalement, un état de mer donné, supposé en première approximation unidirectionnel, est alors caractérisé essentiellement par son « spectre de puissance», c’est-à-dire par la répartition de son énergie en fonction de la pulsation des houles composantes. Des spectres standards sont proposés pour représenter au mieux la mer dans certaines zones particulièrement importantes, Atlantique nord et mer du Nord notamment.

Selon ce point de vue, le navire peut alors être assimilé à un filtre qui, à une entrée aléatoire (la mer), fait correspondre une sortie (mouvements, contraintes dans la charpente...) également aléatoire et représentable sous forme spectrale. Il résulte de ce qui a été dit plus haut dans le cas de la houle régulière qu’un navire est essentiellement un filtre à bande étroite pour le roulis et un filtre à bande large pour le tangage.

Si l’on connaît la réponse du navire aux différents états de mer qu’il devrait rencontrer au cours d’une traversée donnée, il est alors possible de calculer sa route pour rendre minimale la durée du parcours, tout en maintenant les mouvements ou les contraintes dans des limites acceptables: c’est la «navigation météorologique» qui est appliquée sur certains navires de charge, et qui leur permet de réaliser des gains de temps allant jusqu’à 15 p. 100 dans des conditions de mer les plus mauvaises.

4. Qualités évolutives

Les qualités qu’on exige d’un navire touchant sa manœuvrabilité sont d’une certaine façon contradictoires car, s’il doit évidemment pouvoir évoluer dans un espace aussi réduit que possible, il lui faut aussi posséder une bonne tenue de route.

Stabilité de la navigation en ligne droite

Supposons que la barre soit calée à zéro et que, par suite d’une perturbation passagère, le navire soit écarté de son régime normal de route rectiligne. La perturbation cessant, le navire reprend normalement une route rectiligne (pas nécessairement confondue d’ailleurs avec sa route d’origine); mais, pour un navire aux formes remplies, il arrive qu’un tel régime soit instable: ce navire entre alors en giration permanente, soit à droite, soit à gauche, selon les conditions initiales. Un tel phénomène, qui présente des inconvénients certains pour la navigation, peut être combattu en installant un plan mince à l’arrière du navire.

Entrée en giration et giration permanente

Quand on oriente la barre à un angle donné, il commence par s’exercer sur le gouvernail une portance qui entraîne une mise en dérive de la carène; celle-ci se comportant en l’occurrence comme une aile médiocre d’envergure très petite est alors elle-même le siège d’une portance hydrodynamique. Au bout d’un certain temps, le navire finit par prendre un régime permanent de giration caractérisé par un rayon R, une certaine «dérive» (le navire tourne son avant vers l’intérieur du cercle de giration), une vitesse plus petite que la vitesse d’approche, et une gîte vers l’extérieur. À l’angle de barre maximal (30-35⁰ car au-delà le gouvernail perd de son efficacité), R est de l’ordre de grandeur de deux fois la longueur L du navire; il est plus petit pour les navires aux formes pleines (cf. photo) que pour les navires élancés.

Le régime transitoire est, de son côté, d’autant plus court que le gouvernail est bien dégagé de la carène et que la vitesse d’orientation du gouvernail est grande; la distance parcourue par le navire pendant cette phase est de l’ordre de 0,5 L. C’est en général à la mise de barre qu’il faut exercer le couple maximal sur la mèche du gouvernail; ce couple dépend grandement du type du gouvernail et de la position de sa mèche; un gouvernail «compensé», c’est-à-dire dont la mèche passe en arrière du bord d’attaque, permet de limiter la puissance de l’appareil à gouverner.

Manœuvrabilité à faible vitesse ou au point fixe

Le gouvernail, dont la portance est proportionnelle à V ², a une efficacité réduite à faible vitesse. Aussi existe-t-il, en dehors des hélices qu’on doit utiliser au maximum, de nombreux dispositifs spéciaux pour faciliter la manœuvrabilité au point fixe, par exemple:

– les propulseurs cycloïdaux à pales verticales qui permettent de créer une poussée de direction quelconque;

– le gouvernail actif qui, comportant un petit propulseur auxiliaire, permet de créer une poussée de direction quelconque;

– le propulseur d’étrave en tunnel qui crée à l’avant une poussée transversale.

Manœuvrabilité en eau profonde et en canal

Par un effet d’image, la proximité du fond entraîne, en eau peu profonde, d’une part un affaissement du navire qui peut talonner si la hauteur d’eau sous la quille est trop petite, d’autre part une augmentation des forces hydrodynamiques horizontales, favorable du point de vue de la stabilité mais défavorable du point de vue de la giration.

En canal, il existe de plus un effet d’image des bords qui se traduit par une attraction du navire par la berge la plus proche; le régime de route du navire dans l’axe du canal est donc instable; ce phénomène, qui rend souvent délicat le passage en canal, est à l’origine de nombreux accidents. Quand le canal est relativement étroit (cas du canal de Suez par exemple), on est alors amené à organiser le transit des navires en convoi sans possibilité de croisement en dehors de zones réservées à cet effet.

Encyclopédie Universelle. 2012.